はじめに

みなさんは日々何かしらの問題に直面しているとおもいます。

それは、プライベートから仕事まで実に様々なものですよね。
今日の晩ご飯は何にしようかという、比較的解決しやすい問題から、
お店の売上が落ちてきてしまっているからどう対策をしようか、という問題、
そしてもっと複雑な社会の問題に向き合う事もあるかも知れません。

問題の規模が大きくかつ複雑になればなるほど、
意思決定に悩むと思います。

このブログではそんな問題に直面した時、どういう手順で考えていけば、
より早く、着実に解決策を実行に移すことができるのか、
そのプロセスを部分と俯瞰でみていきます！

このブログは2部構成で、全体では以下の内容を扱います。

①ギャップの特定
②課題の導出
③解決策の設定
④実行

問題解決の手順は
①現状とあるべき姿のギャップの特定からはじまり、
②本質的な課題を見つけ出し、
③何かしらの解決策を立案し、
④実行に移す一連のプロセスの流れがあります。

今回は①現状とあるべき姿のギャップの特定と
②本質的な課題を見つけ出す、を説明していきます。

問題解決が必要な時、そもそもの課題を特定する時などにこの考え方が
お役に立てば幸いです！

①ギャップの特定 ~現状とあるべき姿~

まず問題が生ずる時はどういう状態かというと、現状とあるべき姿にギャップがある、
という事ですね。

つまり、現状が理想の状態と等しければ問題はないと言えます。

現状とあるべき姿にギャップがある時にまず行うことは現状の把握です。

As-is（現状の姿）、To be（あるべき姿）モデルとして語られる場合もあります。

現状の把握には様々な方法があるかと思いますがここでは以下の方法で現状を
紐解いていきます。

情報収集

事実状況の把握

現状の分析

シナリオ設計

まず、情報収集から始まります。

必要な情報を存在しているデータから集めていきます。
ここでは発散的な収集も必要ですが、なんでもかんでも集めていくと
時間がかかり過ぎてしまいますのである程度の仮説を立てて、
情報収集をすることをお勧めします。

次に得られた情報から事実のみを抽出していき、
現状を的確に捉えていきます。

そして現状を分析していきます、
定量データのモデル化、定性情報のモデル化を行い現状を把握しやすくします。

シナリオ設計とは現状の問題点を放置しておくと、
どういう状況になるのかをシナリオとして描きます。

現状の把握と同時にあるべき状態、
理想の姿も捉えておきます。

To Be (あるべき姿）の明確化

上位のゴール・目標設定

バックグラウンド（背景）の理解

以上で現状とあるべき姿（理想の状態）のギャップが見えてきた
のではないかと思います。

次は「課題の導出」を説明していきます。

② 課題の導出

ここでは今まで見てきた現状の把握からあるべき姿とのギャップを踏まえて、
課題を捉えていく方法を見ていきます。

実に様々な特定方法があるのですが、ここでは以下の方法を参考に見ていきます。

本質的な原因の特定

• ピラミッドストラクチャー
• ロジックツリー
• 因果関係図

本質的な問題・課題と解決策の基本方向の明確化

本質的な原因を特定する方法として、ピラミッドストラクチャー、ロジックツリー、
因果関係図があげられます。

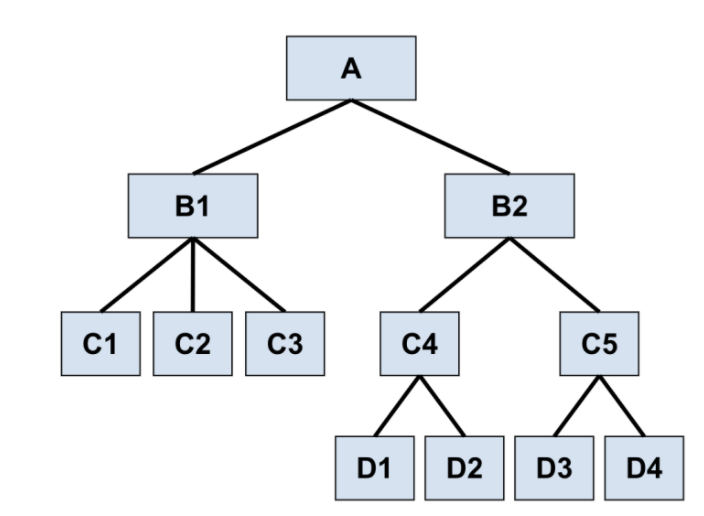
まずピラミッドストラクチャーですが、これは論理構造でコミュニケーションする方法で、ピラミッドみたいに構造化をしていきます。

なぜやるのか、どうやってやるのか、事実や論理を元にして、いくつか書いて、それを元に結論を導いていきます。

この論理構成は口頭ベースだと話しながら修正できますが、何か紙などの視覚化ツールを使う場合、
この論理構成がまとまっていることが重要です。

下図を見ながら説明しますと、

最終的に言いたい結論Aが最初に書いてあって、その結論をサポートするための事実や意味合いが
B-1、B-2というカタチで書いてある、それを更にサポートする事実や意味合いが
C-1、C-2というカタチで書いてあると読み手は負担なく、理解を得やすくなります。

読み手が内容を論理的に理解できるようになるのでコミュニケーションがスムーズになりますし、
コミュニケーションの再現性も高くなります。

続いてロジックツリーですが、

これは課題の解決策の全体像を網羅的に、要素間の関連性（論理性）を表現した図解表現になります。

思考の漏れを発見できたり、効率的に全体像を作ることができ、全体像が見えることで個別要素の優先順位付けが容易になります。他者との情報共有や議論がし易くなります。

例えば「どのように会社の売上を上げるのか？」というテーマを分解していくと、
既存事業の売上を増やせるのか、
もしくは新規事業の売上を増やせるのかと※MECE（ミッシー）に分けていきます。

※MECE（ミッシー）とは漏れなくダブりなくの意味

ここがMECEに分かれていないと漏れがあったところに正しい解があるかもしれない
（機会損失になってしまうかもしれない）ので、漏れなくロジックツリーを組んでいくことが
重要です。

既存事業の売上についてはユーザー数を増やすのか、単価を上げるのかと分解していく。

これを更に分解していくことで解くべき課題を特定して、
そこについてアプローチしていく。
漠然とした課題に対して、それを具体化して解に結び付けていくための
アプローチがロジックツリーです。

ちょっとしたトピックですがドキュメント内でロジックツリーを書くときのポイントを
解説しておきます。

①左から右に行くに従って、概念的内容から具体的内容になっているか、
②ツリーの右側（ツリーの最終地点）が具体的な原因や解決策になっているか
③具体的な原因や解決策が主要課題（ツリーのスタート地点）にリンクしているか
④自分以外の誰か（自分より論理思考能力の高い人）にチェックしてもらう

最後の因果関係図ですが、これは原因と結果の関係性を把握するための方法になります。

事象間に存在する因果関係を発見するには基本的には「結果」である事象を突き合わせて比べ、
同じ結果が生じる前に必ず登場する事象を見つけ出して、それが「原因」であると特定します。
しかし、現実の事象の因果関係はかなり複雑な構造になっているのが常です。

結果としてのある一つの事象も、それを引き起こした原因がただ一つだけである場合は稀であり、
複数の事象が原因として横並びに存在しているケースが多い。

例えば、「A君が難関大学の受験に合格した。」のは「A君の頭がよかった」からだけでなく、
「A君は必死で受験勉強を頑張った。」からでもあり、
また「万全の状態で受験に臨めるよう体調を整えた。」ことも重要な要因とみなすことができます。

そして更に、原因としてのある事象の背景にはその事象を引き起こしたまたその原因が存在し、
そしてそのまた背景には更に深い原因があるというようにいわば数珠つなぎのようにタテにも
因果関係が繋がっています。

「A君が必死で受験勉強を頑張った」のは
「どうしてもその大学のX教授の授業を受けたかった」
からであり、X教授の授業に憧れたのは
「高校の時に読んだX教授の著作に感銘を受けた」
からなどなど、現実の因果はこのように数珠つなぎにつながっています。

そしてこの因果の関係を図解にしていき、どの結果がどの原因と強く直接的に関係があるのか、あるいは間接的にどのような結びつきがあるのかをまとめていくことで因果の関係が把握し易くなります。

この３つのアプローチを用いて問題の本質的な課題を特定して、解決策の基本方向の明確化につなげていきます。

本日はここまでになります！
次回の「論理的に問題を解決する考え方 その２」では
③解決策の設定と④実行を見ていきます！